Estimation Nation

So, it's the day before spring break.  As if that weren't motivation enough (for the students) to not move on with content, there were lots of kids missing and this was an orphaned 'A day' (we're on an A/B schedule, and I have one section of physics and one of honors physics on each of the days, so I have to be careful about missed days in order to keep them together).

So... let's do something fun! (as usual), but non-content oriented (not as usual).  Let's do...

Fermi problems!

Here are the ground rules:

1. No calculators, long division, or long multiplication: stick to 1 or 2 sig figs (maybe the only time I say those dreaded words all year!) and concentrate on getting the right power of ten for the answer
2. No research: you know more than you think you do, and you can figure things out from distantly related facts (remember all of those chains of reasoning that we've been doing?!).  Anything else?  Intelligent estimation.

I presented a big set of questions, and students, in groups, chose a question and dove in.  In the past, I have given everybody one question or assigned each group one question, but I thought that this was more in line with the WCYDWT? spirit that we've been going with this year.

Here's the list of questions (many creditable to Maryland's list), along with student solutions.  Many of the reasoning chains are pretty well-communicated, which is great.  Some haven't gotten there yet, but we're working on it.

• How many piano tuners are there in NYC?
• How many hairs are there on your head?
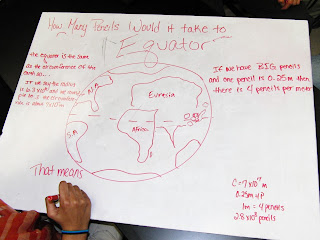
• How many pencils would it take to circle the equator?

• What's "your share" of the land area of the Earth?
• How much (per hour) will you pay for classes in college?

• How many drops of water are there in the Great Lakes?
• How many blades of grass are there in a typical lawn?
• If you remove all of the string from all of the tennis rackets in the US, how far could it stretch?
• How heavy is the rain that falls on the school's roof during a big storm?
• How many hours would you have to work (at minimum wage) to pay "your share" of the national debt?

• If the whole US were a pool, how deep would it be when filled with all of the milk consumed in the US in a year?
• How many flat tires are there right now in the US?
• How long would it take you to reshelve every book in the library?

• Could we build a pipe organ in the classroom that covers the whole range of human hearing?

I thought that it was interesting to look at which ones were popular and which weren't.  Mostly, students stuck to things close to their experience and/or in their personal interest (pencils, tuition cost).  These are also very concrete ideas - easy to get a handle on for students.  At least we have a consensus that it'd take some number in the low hundreds of millions of pencils to circle the equator!  You can rest well during spring break now, secure in that knowledge.

The next time we do Fermi problems, I'll force some engagement with some of these that just seem impossible to them (until they dig in), like the drops of water in the Great Lakes, the number of piano tuners, or (my personal favorite) the amount of water flowing through the Mississippi River in a year.