Quick Labs: AP Physics/Energy

The AP Physics class did a bang-up job on some quick labs about energy on Friday - just a mere 3 days before winter break!  All three projects showed terrific use of revision of their prototype experiments, as well.

The premise of the quick lab is to design, carry out, analyze, and present an experiment during a single 90-minute class period.  Presentations should be a single whiteboard.

The experiments:
Alex, Alex, Brandon 

• They took video of basketball shots, from launch to floor, and used video analysis to determine how much energy the net (all were 'swishes,' of course) took from the ball as it went through. 
• Revisions: initially using the first two points of the video to determine the launch velocity gave unrealistically high results, so they changed that part of the analysis to use kinematics to analyze the change in horizontal and vertical position and time taken (all easily measured from the video) from launch to goal in order to find the launch velocity.
• The boards (yes, they cheated and used two!):

Kawala and Kati

• They slid a small whiteboard eraser down a ramp, after which it plunged to the floor.  To determine the coefficient of kinetic friction between the ramp and the block, they used the fall distance and how far away the eraser landed from the table, along with the ramp length and angle.  This required marrying kinematics, conservation of energy, and the work-energy theorem, and 2.5 gallons of algebra.
• Revisions: they used two different 'floors' to take data, having the eraser hit the actual floor in one trial and hit a crate sitting on the floor in another trial.  The advantage of this is that we can find errors by looking at the trend in the data as the height of the floor is varied.  This is a great check that nothing unexpected is going on, and it was a good thing, because the first value was reasonable, but there were a few little errors to be uncovered.  The coefficients came out negative when the height was changed, so it gave a prompt to find the issues, and now they're confident in these numbers!
• The boards (also two!):

  

Cam, Mike, and Toru:

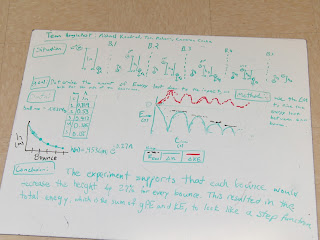
• These guys took some high-speed video as well, analyzing the heights of a bouncing ping-pong ball.  In addition to modeling the height of the ball as a function of bounce (and making a slick argument that the exponential function implies a constant-percentage loss of energy (rather than a constant amount of energy lost), they used Logger Pro to graph the gravitational PE, kinetic energy, and total energy as a function of time, showing the expected constant total energy during each flight (well, a slight decline due to air resistance), with "steps down" in total energy following each bounce.
• Revisions: after considering the parallax issue with measuring the height of the bouncing ball moving in front of a meter stick (especially with the camera mounted to a tripod), they instead dropped the ball next to the meter stick, eliminating the point-of-view issue.
• The board:

Why We Run Towards the Gunfire

We had some scheduling issues last week in physics with visitors, so I made an in-class assessment a take-home assessment.  One great thing about SBG is that there's really no point to cheating on such an assessment, so I think that I'm still getting a good picture of where they are.

On this question, they were (in general) in the weeds:

" Two radio towers 30 km apart transmit synchronized 240 kHz signals.  If a car equipped with a radio receiver tuned to the transmission frequency drives directly from one tower to the other, what will the receiver hear?  Explain; a diagram would help!  Radio signals are light waves that travel 300,000,000 meters per second.

What would the signal be like at a point along the drive that is 8750 meters from the first tower

How would the driving experience change if the radios’ frequencies were changed to 300 kHz?"

We've done some work with 2-source interference, from looking at the "overlapping ripples" diagrams to doing some predictions of frequency from two interfering sound waves given the locations of some points of constructive and destructive interference in the room.

This is the same concept, but a different-looking context, and that's where kids that haven't quite figured out the whole axiomatic reasoning thing have difficulty - yes it looks different, but we can still use the same principles to make predictions about what happens.

In particular, the big message for 2-source interference is that, even though both waves start in phase, they may not be in phase when they reach you, if you're different distances from the two sources.  The difference in travel distance determines the phases of the waves and whether they'll interfere constructively or destructively.  [This type of relationship is familiar: rates (relatives of differences) are famously difficult for students to intuitively grasp - see calculus!]

Back to the story, though:

I collected the assessments at the beginning of class and then posted this problem via projector.  I set the online stopwatch to five minutes and told them to come up with something coherent in their whiteboarding groups. There was a good discussion after that, and we made a lot of good connections.

...before that, though, there was an audible groan when I posted the problem.

Why?  It's a hard problem!  They've already wrestled with it for some period of time, felt anxiety that they were adrift about (da-dum!) an assessment problem, and here I was bringing it up again.

Here's the thing, though: you don't learn anything by running away from those difficult problems - you have to figure them out so that you can use that understanding in the future.  Denial is death in problem-solving.

Soldiers and police officers are incredible because they run towards gunfire, while the rest of us run away.  There's an anxiety-filled and dangerous situation, but they do the harder thing and confront it directly.

In physics (or learning in general), we have to run towards the gunfire too - you have to seek out and fix those misconceptions and misunderstandings.  It's anxiety-filled, too, but one student yesterday noticed a crucial difference between the two situations, when SBG is used: for us, the wounds aren't permanent.  

Not Proficient? No problem - wrestle with the problem, come back, and then you'll be whole again.  Using traditional grading that students are accustomed to, I totally understand why they get gunshy, even at the level of course selection.  Reminding them that this is a safer space for making mistakes has to be a constant occurrence because of that ingrained anxiety, but it's well worth the effort.

One of my favorite demos

I love the demonstration of two-source interference of sound waves - two speakers and a sine wave generator is all it takes to get one of those moments that kids remember for a long while after the course is over (now, if we can just get them to remember why it happens!).

The echoes in my lab aren't too bad, and we can actually map an interference pattern reasonably well, in large areas.  At some point, I'd like to try this in a big space and have them mark nodes (quiet points) and antinodes (loud points) with cones or something, and see if we can recreate the classic illustration.

In the meantime, we mapped out a few points that were relatively easily found:

At this point, we already knew all about order lines and how these loud and soft points came to be; we had analyzed a diagram of the interfering waves, determined where constructive and destructive interference were happening, and noticed the pattern in the 'lines' of nodes and antinodes (and even brought those shapes back to the base definition of a hyperbola!).

This was their first chance to apply that to a live problem: what's the frequency of that annoying hum that I'm playing through the speakers, anyway?  Are these measurements all that we need to determine that?  After all, there's nothing about time here at all, so determining the frequency seems daunting at first.

"What order line is that first soft point on?" is the real catalyzing question that I ask the groups a few minutes into their whiteboarding, if they haven't figured out how to apply the two-source model yet.

From there, there are a few steps of reasoning, some triangle manipulation, and some unit conversions needed.  The triangles and unit conversions shouldn't be an issue at this point, though they still are for some that haven't reached an unconscious competence level.  These assumed skills can really derail you. Especially if a problem is already difficult enough to tax your faculties to the max to begin with, adding a protracted wrestle with a unit conversion or diagramming effectively is likely to push your brain into a useless fried state (like okra).

Once we've connected that the order number is important, that connects to something about the distances from the speakers to the point, so we need to find those distances, using the Pythagorean theorem:

OK, great, but what does the order number tell us? This is a place where the sound is quiet because there's destructive interference, which happens because the waves travel different distances to get here.  The waves began synchronized, but since they've traveled different distances, they're at different points in their oscillation between high and low pressure (they're out of phase).  At this place, the wave from the left speaker has traveled half of a wavelength further than the wave from the right speaker (that's the .5 in the order number!).  Now we know two different ways to write the difference in travel distances:

 

Now that we know the wavelength, we're all set:

That's quiet a chain of thought there - let's trace the inferences that you have to make to solve this problem:

That's quite a set of inferences and observations, each necessary to solve the problem.  This number of inferences and observations is necessary for many problems that students try to solve, but we don't often think about the chain of logic so literally.  A great deal goes on behind the scenes... or doesn't.  Note too that there's knowledge from previous courses, previous terms and units of this course, and the current situation, but that it all has to fit together; this doesn't happen if students view understanding as disposable.  That sort of mindset is like tying your leg to a tree and trying to go for a run - no matter what direction you go, you can only go so far.

I think that, if students can get comfortable spelling out their reasoning like this, then they can get better at making a linear argument, which is what all problem-solving is - each step must be supported by knowledge or information and must lead to the next step.  Scatter-shot thinking is rampant, and it does not help problem-solving.  Perhaps conscious effort on constructing a "chain of reasoning" can help a student be able to do this type of thinking unconsciously, too!

SBG: Changes for the Winter Term

An informational post, mostly for the benefit of students in my courses:

This winter, we'll be implementing a few changes in our standards-based grading system, in order to streamline the reassessment system and reflect the larger number of standards assessed in the second term.

• Reassessment requests must be made through this Google form: Reassessment Form.
  • The reassessments, at least at the beginning of the term, will be given on Mondays, Wednesdays, and Fridays (let me know if there's a scheduling issue for you)
  • You need to complete the reassessment form by the previous M, W, or F; for example, if you'd like to reassess Monday, you need to complete the form by the previous Friday.
  • The form asks about the preparation that you have done in order to earn reassessment. Corrections are, as always a minimum, and you need to bring the written work that you have done to prepare for the reassessment.
• The grading scale for standards will be a little more detailed this term, adding 'half levels' between NP and De and between De and P, in order to have the grade give a finer level of detail about your understanding.
  • A: Advanced
  • Pr: Proficient
  • P-: Proficient Minus
  • De: Developing
  • D-: Developing Minus
  • NP: Not Proficient
• As there are more standards this term, a single NP will only limit your overall grade to a maximum of C+, rather than C-. Any scores below P will still limit your grade to a maximum of A-.

For full details, check the SBG page on wikiphys.

Capstone 1: Final Paper

Alex has finished our first capstone of the year.  This is also the first post for CapstoneLearning.org; great analysis, Alex!

Abstract:

In this paper I explore the physics of the computer game Osmos.  It was my goal to see how accurately Newton’s laws applied to this game.  I captured video of the game and used Logger Pro to analyze the physics of how an object propels itself by expelling some of its mass in the opposite direction.  I discovered that impacts between random objects have perfect conservation of energy; when the main mass controlled the player moves conservation is not conserved.  In that situation, the player is given approximately four to five times the amount of energy dictated by Newton’s laws to make the game easier.

Full paper linked here.

Three Representations

Today the honors physics classes took their first crack at connecting three of the four representations of interactions: system schemas, free-body diagrams, and motion graphs (v vs. t in particular here).  Along with net force equations, these will be the basis of most of the rest of the year!

We had some great whiteboard meetings as we split into five groups to construct our representations and then made sure that all of each group's representations agreed in each situation.  This is good practice for looking at your own work - multiple representations not only give you multiple avenues to attack a problem, but also let you check yourself!

I encouraged them not to write these down on the sheets that I gave them with the setups, so that they can use them as independent practice later, checking back to the whiteboards for verification afterwards.

For each situation, the students evaluated each representation while the box was at rest, being pushed (and speeding up), and after it is released (after having been pushed).

The four situations were:
A rubber-bottomed cardboard box with a block inside it, on a rough floor.

A cardboard box with a block inside it, on a rough floor.

A cardboard box with a block inside it, on a smooth floor.

A cardboard box with a block inside it, on a perfectly frictionless floor.

 

 

A follow-up task for my students:

Draw v vs. t graphs for each of these four situations on the same set of axes, assuming boxes of equal weight and push forces of equal and constant size.  Here's a template, along with a color-code, ready for magic markers!

 

Along the way, we had a great discussion about what happens to our system schema if we split the box and the block inside it (leading us to our first encounter with static friction!), and about what we can't tell about the motion from free-body diagrams (like... the direction of the motion!).

Thanks to Kelly for the great springboard to this one!

Capstone Project 2 - Comments Wanted!

Kawala has submitted her draft of a capstone project on roller coasters. 

The draft is available here, and she'd love your thoughts!

How Good Is That Number?

When we calculate anything, we're always modeling - we're making assumptions and approximations, and our measurements are always inherently uncertain to some degree.  Our calculation must therefore be viewed with an understanding of its limitations and biases (not the colloquial term implying that there was an agenda, but rather any sort of consistent skew to the results due to some physical mechanism that wasn't accounted for).

One experiment that we did to determine the speed of sound a few days ago is a great case study for talking about error analysis. 

The Goal: We were trying to determine the speed of sound in air.

The Setup: Students spread out across a large field, at known distances from a student with a baseball bat and ball.  The student tossed the ball into the air and hit it.

The Measurement: Students started their watches when they saw the ball hit the bat and stopped them when they heard the impact - the travel time delay and the distance can then be used to determine the speed of sound.

Sources of Error: Again, there's a difference between everyday use of 'error' and scientific use; we don't mean 'mistakes' - if you made a mistake, then you need to fix it.  We're talking about consequences of our modeling assumptions and unavoidable measurement uncertainty.

In this experiment, two big sources jump out at us, and illustrate very nicely the two main forms of experimental error that students are likely to encounter:

• Timer error - every time you start and stop the watch, there's some uncertainty in that measured time interval.  You could have started or stopped a little too late or early, and it's impossible to tell which happened in any given measurement, just based on that one time.  This is a random error source, because it could make your measurement either too high or too low; it generally serves to scatter your data - some points are a little high and some a little low, but the trend is unaffected.
• Reaction time - this one's more subtle here, and a diagram really helps to illustrate its presence in this case:

 

          The subtle part is is the difference between the two events.  We saw the impact coming - he tossed the ball into the air, and we could anticipate the impact, so the beginning of the time interval came as absolutely no surprise to us.  The end of the interval, however, was subject to our reflexes; you can't hear the ball until the sound gets to you, so there's no way to anticipate the moment at which you should stop your watch.  This tells us that the measured time intervals will all be too long - that's a systematic error source, because it skews all of our data in the same direction, and has an effect on our average value. 

Effects of the error sources:  This is the most important part of the error analysis, because it gives us information on how we should trust our final calculated value.  In this case, we should expect our calculated speed to be lower than the true value.  We could quantify how much longer, but that's a bit deeper than I'm interested in going with this physics class.  If we can qualitatively analyze the effects of error sources, then I'll be thrilled!

• The reaction time issue will cause our times to be uniformly too long, which will cause the speeds to be too low.  This is a systematic effect, and we should expect the average value to be lower than the true speed of sound.
• The timer error will scatter our values, but not affect the average value; some will be too high (because the times were too low) and some too low (because the times were too high), but there's no effect on the average speed.

 

Now This Is a Great Design

I usually begin our discussion of waves by tasking the students to design an experiment (as a class) to measure the speed of sound in air.  It's a backdoor way into experimental design, error analysis, and rate analysis, rather than really particularly wave-focused.  There are a variety of factors that make this difficult, not the least of which are the high speed of the wave (necessitating large distances) and the issue with measuring an event at a distance (made necessary by the large distance).

One of the slickest ways to get around this is by synchronizing watches, spreading out over a distance, and stopping the watches as each person hears a lour sound.  The differences between positions of the timers and the differences in times can be used to determine the speed - most easily by fitting a line to the position vs. time data, where the slope will give the speed, magically using all of the data in a single calculation!

A very creative design this year came from a couple of groups, actually:

• Stand some distance away from a wall
• Clap

... I've heard this one before, up to this point.  Generally, the problem comes when students try to measure the delay of that echo, which is really short.

• Clap again, when you hear the first echo
• Repeat, repeat, repeat...
• By counting claps and timing, say, 50 of them, determine the travel time for each echo.

That's a slick design, and applies some of the good measurement techniques that we've learned to apply to timing oscillations - nice work! It takes a few cycles to get your clapping tempo to match the travel period, but after you're synched up, you can take data on this pretty easily.

Our data:

• Average time of 13.43 seconds for 50 clap cycles (51 total claps!)
• Distance from the wall: 42.8 meters

There's an easy mistake to be made in the analysis, which a diagram will sort out:

The distance traveled during the time between claps is twice our measured distance; you have to make sure that the time and distance that you use to calculate the speed are for the same motion!

With an average travel time of .2686 seconds, and a distance traveled of 85.6 meters, our calculated speed of sound is... 319 meters per second!  That's pretty good for a really low-tech method, I'd say.

Post-game Reassessment: Instant Feedback

A few days ago, I posted about our first use of Frank Noschese's system for instant post-assessment feedback.  The highlights:

• After finishing the assessment, students go (with paper in hand, but not pencil) to one of the exhaustively completed keys around the room
• Students pick up a green pencil and mark on their papers: what they were thinking while doing any analysis that came out incorrect, what they can do better next time, and even alternate ideas for analysis if theirs was already correct, but not the same method(s) that I used
• Students hand in the paper to me, I grade them, record the grades and feedback, and return them as usual

From my point of view, students are looking at their own work right in the moment, so they have immediate buy-in and a fresh memory of what they were thinking while doing the problem, so it's much easier for them to identify their errors in thinking (rather than their errors in doing) than it is for me to try to guess what they were thinking, given only what they did.  Writing their own feedback also helps them have automatically meaningful input for future reference.  I add in anything that I think that they're still missing, but they're doing most of the work here - as it should be!  Learning, unfortunately (for efficiency, fortunately for fun!), isn't something that anyone can do for someone else.

Well, those were my thoughts and hopes.  The next class, I asked students to give me some of their feedback, to see if they saw it as I did.  From their papers on assessment day, I saw a surprising depth of self-reflection and it seemed (from my POV) to be successful.  From their point of view:

• "I thought it helped me to understand problems/errors I made while the problem was still fresh in my mind.  It was Good + Useful!"
• "I thought what we did helped a lot because it showed me what I need to work on for the test."
• "I think the green pencil was helpful because it allowed me to learn from my mistakes."
• "It helped me understand some of it, but it was a little difficult to know if I would get partial credit, like with tangent lines, but it did help me understand what went wrong" The small wrinkle that they were drawing tangent lines by hand to determine velocity from a curved position graph meant that some students had difficulty judging what was close enough.  The partial credit thing is really ingrained in them - focus on the learning, not the points!
• "Good, so you know right away what you did wrong and fix it."
• "Was not helpful because I did not understand what to do."
• "This method was kind of helpful because it forced me to look at my mistakes but sometimes I don't know what my mistakes were."
• "I liked it because it helped me learn what I did wrong."
• "I liked the idea.  My thought process was fresh in my mind."
• "Now I know what I was thinking on the test.  This is positive so I realize what I was thinking during the test."
• "I liked it! It helped, I think, and I could see my mistake as soon as it happened and know where I went wrong."
• "For the first side the numbers were slightly different but the method was the same, so it confirmed my procedure.  The other side showed how I messed up the equation slightly."
• "I liked doing the green pencil because it was right after the assessment so I knew what I was thinking while taking the assessment."
• "I thought that going back and making corrections on the assessment immediately after taking it was very helpful.  I could figure out what I did wrong and then use the corrected version to look over and study from.  Also, I know what types of mistakes I made, so I know what to watch out for in the future."
• "I liked it.  It was good to see my mistakes right after."
• "I liked the idea a lot, but it didn't really help me since I had the answers right."
• "It helped me learn what I did wrong to see the work."
• "It helped me pinpoint what I needed to work on."
• "It helped. When I got my quiz back, I recognized what I was thinking when I took it."
• "I think it was nice because I could look at the correct answer and see why it was wrong instead of you just declaring it was wrong and not showing us exactly."
• "It was hard to tell exactly what you did wrong or if you needed more information than you had." My key was very verbose - some kids did ask if they needed to show all of the work that I did. 
• "It was good feedback."

Habits of Great Problem-Solvers

We're wrapping up CAPM (constant acceleration motion) in honors physics, and one of the biggest ideas is determining the direction of an object's acceleration.  It's very important once we start moving into force analysis, because it tells you about how the forces acting on an object are related, and sometimes tells you the direction of a force that you couldn't determine any other way (static friction, I'm looking at you!).

We took a second to stop and collect our list of ways to determine the acceleration of an object:

• From the x vs. t graph: is the slope increasing or decreasing?  You have to be careful here to differentiate between getting steeper vs. flatter (which tells you about speed) and whether the value of the slope is increasing or decreasing (going from a zero slope to a negative slope is decreasing).
• From the v vs. t graph: is the slope positive or negative?  There's your acceleration sign direction, too.
• From a diagram: is the object speeding up or slowing down, and what direction is it moving?  The combination of the acceleration and velocity directions determines whether something's speeding up or slowing down, so you can work backwards to find the acceleration direction from the directions and relative sizes of the initial and final velocities.  If you know that it's moving left and speeding up, you know that the acceleration's left as well.  If it's moving left and slowing down, then the acceleration is in the direction opposite the velocity (so a is to the right, in this case).
• From the x vs t graph: is the graph concave up or down?  That is, does it open upward or downward?  Positive accelerations have concave up position graphs.

We applied this to an easy example using a ramp and a Pasco Visual Accelerometer.  These are pretty neat little boxes that produce a green arrow or a red arrow to one side or the other, based one the direction in which it is accelerating.  For some reason, kids will believe that little computer box with all of their hearts.

The second challenge was a little tougher: I roll a cart up the hill with the visual accelerometer on it, and let it go up to the top and then come back down.  I asked the students to predict the direction (or directions) of the acceleration, and to defend their answers with at least two pieces of evidence (they have four possible lines of inquiry from our four methods above!).

This is one that always has the potential to stump my students.  Detaching the directions of velocity and acceleration (indeed, differentiating that velocity and acceleration are actually two different things!) can be tough, as can detaching speed from velocity.

Which direction is it moving? You can't tell by this acceleration reading!

They did very well with it, though, with most groups coming to the correct answer rather quickly and confidently.  A big part of this seemed to be their use of these multiple lines of evidence to back up their decisions.  Every approach that you take to a problem will give you an answer.  Whether that answer's worth much?  It's hard to say, if that's all you have to go off of.  If you can attack the problem from multiple directions, then you can really have some confidence in it.

I definitely had groups draw iffy motion graphs during this.  Most groups, however, as they used the diagrams and graphs to try to come to the same answer over and over again, noticed when one representation gave a different answer than the others, and were able to flip that velocity graph or look at the starting position more carefully.

This is what great problem-solvers do - they use multiple avenues to address a problem, letting the results of each one inform the others.  It's not really a linear process, but an attack from multiple angles, until you break through, and then a mopping-up of all of those open threads, in order to make sure that everything line up as it should.

Once again, we see that:

Great problem solvers don't always get it right the first time - they just catch their own mistakes, so that the first answer that you see from them is right.

 This idea about the non-linearity of problem solving doesn't just apply to problem-solving, though: the whole web of knowledge in your head really is a web.  If you only connect each piece of knowledge to the next in a single chain or ladder, then it's difficult to tell when a thread breaks.  After all, you'll always get an answer.

If, however, each piece is connected to many others, then one strand breaking isn't an issue, because you have several other ways to make that connection.  This is really the secret of complex problem-solving, and pretty much the definition of knowing something cold (unconscious competence!).

Here's a web that I threw together for my knowledge connecting the kinematic quantities:

The most fundamental thing that makes my understanding deeper than the honors students' understanding at the moment is that I just know some more connections than they do (so far).  Making this web as rich as possible is really your job as a learner.  When teachers bemoan "surface understanding," cramming, and answer-hunting, it boils down to a difference in the process for a student - that student's goal directly impacts the level of understanding that he/she'll get out of the course.

So, how about it?  Are you trying to get someone to tell you "the path to the answer," or are you building your own sprawling web of highways?

Capstone 1 Unveiled! Comments Wanted!

The first capstone draft is out!

Alex has done some analysis of the Osmos video game - his capstone paper draft is linked here.  Take a look, let him know what you think.  After revision, this will be posted at capstonelearning.org , a capstone aggregation site so cutting-edge that there hasn't even been a post yet!

Post-Game Analysis, Part 1

I've been following John Burk's and Frank Noschese's ideas about "post-game analysis" (that's what you do after an assessment).  Too often, we just move on like nothing happened, and so the students do as well.  Unfortunately, asking "are there any questions?" and doing a few solutions on the board yourself has several problems: you're probably only addressing a small proportion of the kids at any given time (so they tune out), you're doing the work, while they're passively receiving (that didn't work for them the first time!), and it can take forever.

It also happens on the next class day, which can be as much as three days away, with our every-other-day schedule here.

There are also the traditional problems about feedback from me - many don't read it (hopefully fewer than before I started really talking about mindset and normalizing mistakes often), it takes a long time for me to write, and I might end up writing less than I'd like because of the time demand and effort required.

Here's a big one: my feedback, even if it's as long and detailed as I'd write in the ideal world where I have only one student (and 15 free periods and a boat), is based on what I think your issues are, based on what you wrote, which may not bear much relation to what you're actually thinking!  After three days, do you even remember what you were thinking?

I gave the immediate post-game feedback a try this week, on our first assessment for graphical models of constant-acceleration motion.  It was basic stuff - using slopes and areas to go from one type of motion graph to another, but there are lots of little places to not have it go quite right.  The kids did well overall, but most people had one or more little issues with the execution.

After they finished the assessment, they went to one of the three keys that I had made (these took a little while, because I was super-explicit about every piece of physics and logic) and used a green colored pencil to write down what they were trying to do and what they should've been doing for any places that they had mistakes (well, that was the goal - most did pretty well!).  Only they know what's going on in their heads, and they won't remember later, so this seems like a great opportunity to capitalize on their attention and motivation, and to let them write comments that are the most helpful to themselves, instead of me guessing what they were thinking/what they need to hear.

Here are a couple of terrific examples of post-game work from a student.  Notice how I don't really have much to say, because she has done all of her own 'fixing'!

I'm going to ask them today to give me some feedback on how well this worked for them.  I'm thinking that I'll do this with the first assessment or two for each standard, as a way to get their early mistakes and misconceptions dealt with more quickly.

Fluency = Awesomeness

Another term for the unconscious competence that we've been talking about (here and here) in class is fluency.  In language, fluency is about being able to do a lot of the lower-level skills (pronunciation, grammar, vocabulary) automatically: you're only focusing on the content - on the meaning.

That's the goal is math and science, too.  Too often kids get stuck on and obsessed with the tools (prefixes, scientific notation, algebra, trig, calculus, definitions, moles) and miss the forest for the trees.  Having to spend a lot of mental energy on those things also means that you simply don't have the stamina to get to the end of something with a lot of sub-parts, because the sub-parts require too much effort (because you can't do them fluently!).

We worked at this fiendish challenge problem from The Physics Teacher today. 

Mainly, I wanted to illustrate the concept of looking at different cases or regions within the problem.  Here, we had to consider cases in which neither block slipped, only the bigger block slipped, or only the smaller block slipped.  Cases in which both blocks slip are ruled out by the ribbon's masslessness (think about it - it's a little subtle!).

We went through what the accelerations of each slipping block and non-slipping block (+ribbon) would be in each of the three cases, as well as what the static friction force on each non-slipping block would be in each case.  If a scenario is impossible, you'll get an impossible result from the comparison of the net force required for the acceleration indicated and the acceleration that the static friction /gravity can provide.

It looked something like this:

That's quite a bit of algebra, but... how long did it take us to come up with these functions for all of these different cases? 10 minutes, maybe!

The reason is fluency.  These kids would've taken forever to get these out last year, and would've made a lot of wrong turns and not noticed for a while, because they were still stuck with partial fluency on some of the skills needed to write these equations.  By my estimation, these are the skills that the kids had to be fluent with to model these three situations so quickly:

• Identification of forces (normal, mg, kinetic and static friction)
• Identification of acceleration direction and which accelerations will be equal to which others
• Trig and vector components
• Rotation of axes
• Defining positive in a consistent way for both blocks
• Newton's 2nd law
• Requirements for static friction to be in effect
• Symbolic algebra
• Relationships between the friction coefficients
• Inequalities

Sure, you can explain this problem from the ground up to your mother (well, maybe yours is good at physics: how about mine?), but what if you also have to explain all of those ideas?  It's just a losing battle. 

After all, no composer can write an opera if they have to do "Every Good Boy Does Fine" to know what the notes are!

Another Reason for Reassessment

In a recent post, I talked a bit about this continuum of understanding/stages of learning:

• Unconscious Incompetence
• Conscious Incompetence
• Conscious Competence
• Unconscious Competence

One big reason that you want to get to UC is that you'll be building skills on top of earlier skills; if you're wrestling with motion (CVPM, CAPM), it'll be difficult for you to confront a situation where you're not interested in the motion, but with things that change the motion (forces, momentum, and energy analysis all presuppose a real fluency with motion!), you'll be stuck spending a lot of effort in the wrong place.  Imagine how difficult it'd be to make sense of Killer Angels if you had to sound out every word.  The more that you can 'automate' skills, the more mental effort you'll have left to deal with the newest skills.  This can really derail a physics student!

Another importance reason for getting to the fluency and automaticity of the unconscious competence stage of learning is retention.  Not only is it easier to apply a skill which you have mastered to the point of not needing to consciously think through it, but you'll also retain that understanding longer.

When you really know something, it sticks with you for a long time.  Cramming, on the other hand, might (probably not in physics!) get you to conscious competence, but that level of understanding isn't nearly as stable.  At that point in the learning process, you know quite a bit and can do quite a bit, but you don't have the perspective to put all of the pieces together.  It's not until you can do problems in multiple ways, explain where things come from, and what other phenomena they influence that you're really there.

I think that it's all of those connections that help you retain this level of mastery over a loner period of time.  A strand here or there may break, but if everything's interconnected in your mental model, then there are more strands to help to hold it up, and you have a basis for reconstructing that lost knowledge for yourself.

If you've struggled to gain even a minimal level of competence (consciously incompetent), then your understanding is fragmented enough that it will be all be gone in a matter of a few days or weeks, and you'll be back where you started.

After all of the hard work that you put in to understand a subject, it's wasteful to let it slip away!  If you're not mastering the material when the big assessment/test rolls around, it's crucial for you to address that right away, because the situation will only get worse.

The lower your level of understanding is, the faster it erodes.

Apart from concern for grades or concern for building later knowledge on a firmer foundation, it's vitally important to do some work to maintain or increase your understanding as a defensive measure against losing what knowledge you already have!

Capstone Proposals: Feedback wanted!

The AP Physics class is working on their first set of capstone project proposals.  These are more independent explorations that show a student's ability to synthesize concepts, formulate questions, and apply physics in "real world" scenarios.  The final product will be narrative summaries of the design, results, and interpretation; we'll post those for feedback and revision as well.

Here's where you come in: these are draft proposals, and need feedback.  There are great ideas here, but they need focus, specificity, and a devil's advocate about measurement and design issues.  Comment early, comment often!

The draft proposals, in no particular order:

• Kati:
• Will hitting a field hockey ball with no follow through affect the motion? Will how far I follow through affect the motion of the ball? Will the ball accelerate more? I plan to test the velocity of the ball with and without a follow through. Then see if there is a greater acceleration with more follow through.   
• http://www.youtube.com/watch?v=3uoWvI9hS84 
• the first swing in this video is what I will do but I will not be in motion.

• Alex C:
• My capstone will be analyzing the physics of the computer game Osmos.  In this game, a mass accelerates by 'shooting' part of its mass in the opposite direction.  I am going to analyze whether these separations agree with the conservation of momentum.  I will also being seeing if they do this in one, two, or three dimensions.

• Alex K:
• In the 2007 X-Games, skateboarder Jake Brown was launched 50 feet into the air, lost his skateboard in flight, and consequently slammed onto the flat of the ramp. I want to calculate the acceleration of his head in order for it to come to rest. From the various videos, I know the maximum height in which he reaches, and I can find his velocity. I can therefore find his velocity just before contact.
• To find his velocity, logger pro will be used. Using toolbox equations I can calculate his final velocity just before he hits the ground. I can then model his (non-constant) acceleration using logger and find a function of the acceleration of his head.
• MEDIA:  http://www.youtube.com/watch?v=CTeXKHkNqgk

• Mike:
• I have two ideas for capstones. One is to determine how far down the pellet from my air rifle will drop when aiming for a target that is 100m away, then use this data to determine how much higher above the target I would have to aim when the scope is calibrated for 30m to hit a target is 100m away. 
• Second is to determine which of my kicks a roundhouse, side, front, axe, back, jumping roundhouse, jumping side, jumping front, or jumping back kick exerts the most force. I would determine this by taking the average force between 3 of the same type of kick on a punching bag. 
• I would appreciate your feedback.

• Toru:
• In an iphone app called “Tiny Tower”, there exists a ridiculous elevator. This “Infini-Lift Lightspeed”  elevator has an extreme acceleration rate that can injure the rider when it tries to stop. I will find the acceleration value and the force on the rider by scaling this app to the real world. With the newly found, I will find the movement of the rider when the elevator comes to a complete stop.
• The link to the video that shows how fast the elevator moves 
• http://www.youtube.com/watch?v=-AL6GIIthYU

• Cam:
• For my capstone project, I will build a roller coaster on Roller Coaster Tycoon, and graph the acceleration and position of the rollercoaster based on the velocity which is given.  I would build a simple wooden roller coaster that consists of a chain hill that goes into a steep drop, goes up a steep hill, takes a 180 degree turn and go back down the steep hill, go up 2-3 smaller steep hills based on how long the chain lift is.  The coaster will then take one last 180 degree turn and then head straight into the station.  With knowing the acceleration and velocity of the roller coaster, I will try to determine how long the roller coaster is by using kinematic equations to find the delta X of the roller coaster.  I will be able to check my answer by looking at the data page of the roller coaster, which lists the ride length among other things.

• Brandon:
• The defensive lineman hits an average joe. The footage I will be using is on the link below between time 4:26 and 4:36. I will be calculating the direction and the size of the force needed to make that hit happen. The average joe is 5' 6'' 160lbs. and the 6'5'' 360lbs. And also what the force is on him has he hits the ground. 
• http://www.youtube.com/watch?v=2QOEIQ3_Kuo&feature=related

• Kawala:
• 
  Question: To test the roller coaster slows down when passing the second hill than passing the first hill, which obeys the principle of conservation of energy.
• Physical principle: Conservation of Energy. The car has initial kinetic energy when it starts so that it can go up the first hill. Then the potential energy turns to kinetic energy as the car goes down the hill. The further it goes, the more energy is transformed. The car has the maximum velocity at the bottom of the hill. As it goes up the second hill, the kinetic energy turns back into potential energy so that the car slows down. This also proves that the second hill of is designed to be lower than the first hill. The car cannot reach the same height as the first time because the energy is decreased due to the friction.
• How to approach: From the video I found, I can scale and use the logger pro to determine the velocity at different points. Also, the formula of the conservation of energy and kinematic equations can help to find some of the variables. Derivatives and Integrals might be necessary
• Quantities: Initial velocity, final velocity, the radius of the loop, the mass of the car, g

A Great Discussion and a lot of Abbreviations

First: honors physics had the best discussion today.  We went through some graphs, practicing whether they told us about a CVPM (constant v) motion, a CAPM (constant a) motion, or neither.  It's pretty early practice in our CAPM unit, so we're just learning the ropes of what each graph says about the motion.  This was our set of graphs (thanks to Minds On Physics and Kelly O'Shea):

We've done some modeling of carts on ramps, finding functions for the final velocity as a function of delta t and seeing the shape of x vs t), so that was their background with accelerated motion (that, and the curve in our error analysis of... well, I'll save that post for another day).  Everything was smooth sailing until one unlucky soul got graph H. 

After a bit of fumbling to an answer, I opened it up.  They were all opened up for questions, but this was the one the everyone was unsure of.  After a few minutes of half answers followed by examining of my face for feedback (that wasn't forthcoming), they really engaged with each other.  Discussions are really easy to have between each kid individually and the teacher, but it's difficult to get them to discuss with each other, particularly when the topic's not subjective.  The biggest key is for me to shut up.  It's hard to do, but a little patience will see them start to really turn their brains on. There's a correct answer here, but what is it?  The tipping point here is when they start actually listening to each other - you know you're there when they analyze the consequences of someone else's argument, and it's a beautiful thing.

     But isn't it easier if I just confirm/deny their answers, and let everyone know what the correct response is?

It depends on what you mean by easier.  Easier for me? Yes. Quicker? Yes. More comfortable for them? Yes.  Better for them to learn how to reason through an unfamiliar situation? No.  Better for them to build a mental model of the process?  Not even close.

Atul Gawande (I'm linking to John Burk here, because that's where I heard of him) has this thing about stages that learners go through: he identifies them as Unconscious Incompetence, Conscious Incompetence, Conscious Competence, and Unconscious Competence (there's a great scene from Waiting for Guffman on this topic...).  I'd sum those up as:

UI: Clueless - doesn't know what the game is

CI: Knows the game, can't play it well

CC: Can do it, but have to think about it

UC: No sweat - like second-nature

The trick about this progression (well, there are two, but the second one I'm saving for another day!) is the frustration and self-confidence swings during this journey.  I made this graph to sum it up:

 

• The understanding increases as you move from level to level, but you'll always have plateaus that you'll have to break through.
• Your confidence really takes a hit as you figure out what you don't know (conscious incompetence), rebounds, and then goes off the charts as you really figure it out.  This is one way to get a handle on where you are on the chart: if you have apprehension, you're not at UC (but you might be at UI!)
• The frustration of going from unconscious incompetence to conscious incompetence can be brutal.  You have started to learn how little you know, and the hill can seem steep.  This, however, is the only way through to competence of any sort.  Ignoring this (by having passive study or avoidance) does not fix the problem.  There's some frustration in clearing the last hurdle, but much less, because your confidence is bolstered by having competence in the material already.

There's a connection that I make here to that study (which I still can't find) about preparing for an exam by passive study or a period of time, cramming, and taking a test.  The test-takers were best prepared (now they really know what they do and don't know), but least confident. That confidence can be a bit of false internal feedback.  You have to be aware of it, push through it, and know that good times are on the other side. 

I see a lot of skills that should be UC for students (like algebra, graphing, writing) take the forefront as points of difficulty; maybe they studied to become consciously competent for a test a few years ago, but that's not enough when you're trying to build on those skills.  You need to be able to do them without thought or hesitation - you need to be unconsciously competent.

Maximization and an Awesome Connection

Last week, AP Physics took kinematics to the max (or min).  The prompt for the day:

     Pick a situation and maximize (or minimize) something related to a motion.

In a few small groups, everyone ended up landing on trying to find the angle that maximizes projectile range down (or up) a hill.  This is a fun problem, and really tests the algebra/bookkeeping skills.

This is also a good chance to test out not one but two cool applications of the quadratic formula.  You have a couple of equations that are quadratic not in theta but in the tangent of theta!

Getting all of the way down to the end requires some slick tricks like that, but also a great deal of discipline and the ability to work quickly but very accurately.  Thinking back to my undergrad physics courses oh-so-long ago, I remember that being an under-advertised but very important skill.  The whole idea of junior-level mechanics and E&M and certainly of undergraduate quantum mechanics seems to be to exhaust all of the problems that can be done analytically, which means that they get... ahem... robust, in terms of the algebra.

One group finished quickly enough to test their prediction with a ball launcher and looooooong ramp:

The prediction worked like a charm, and the ball's maximum range occurred at the predicted launch angle.  They made some pencil marks (did you guys erase those?!) on the track, and here was where it got real.

Even though the maximum range did occur at the predicted angle, they noticed that the range didn't change much even with what seemed to be a relatively large angle change.  It decreased, just not as much as they had expected.  On one side of the optimum angle, the range changed very little for up to 10 or 15 degrees of angle change; on the other side, it was significantly more sensitive.

This observation led to a couple of great revelations (without any input from me):

• This tells us a good bit about the shape of the function.  On one side, the function slopes away from the maximum relatively slowly, but falls off much more quickly on the other side
• This is, 100%, the "algebraic test" for extrema!  OK, we may have made that name up, but it's the process where, instead of taking a second derivative to test the type of extremum you've found, you test a value to the left and one to the right.  This test works well if the derivative's complex.  Visually, this is it, in the flesh!

That connection - the idea that we can just see what some arcane mathematical procedure is about by doing an experiment - is fantastic.  I'd love to take credit for having designed the whole situation to force that epiphany, but it just happened.  That makes it even better!

Let me tell you about units...

Sometimes students think that units are for me.  I get all excited about them writing down and checking their units.  "It's a chance to catch your mistakes," I say.  "It's a chance to really know what the units in the answer are," I say. "It can tell you how to do the problem!" I exclaim.  "Come out to the coast, we'll get together, have a few laughs," I say (wait, that wasn't me).

Anyway, the students that see it, buy it, or try it... succeed.  Those that refuse... generally struggle (certainly, they struggle more than they need to).

I get that you might (should?) need more than my word to buy into something.  That's where the logical argument and all of the times that we've seen it work in HW and class should come in.  If that didn't do it for you, then how about this?

On our first assessment covering amplitude of oscillations, I asked this question, after showing a video of a lab cart oscillating with the help of two horizontal springs.  They had already determined the amplitude at my request, and had stopwatches available.

     "How far would the cart travel in a year, if its amplitude remained constant?"

Yes, it's not terribly 'real world,' because the cart certainly won't go that long, with all of those juicy damping forces around.  That's OK - we're just stretching our legs a bit.

What I like about this is that it connects period/frequency and amplitude.  That, and we'd never done anything like it before.  There's always something new on a physics test, but you can apply old concepts to figure it out.  That's just... how physics works.  If you're waiting for me to list all of the "types of problems," then you'll be waiting a long time.  The concepts that we apply to this multitude?  Well, you can list that pretty easily (it's the list of standards for the term!).

Anyway, here's where the units hit the road.  Folks that have taken my advice and really gotten into checking their units had a real advantage:

     Not only did unit-checkers get all of the more familiar applications of T, f, and A correct, they also all got this entirely new question correct!

Yeah, all of them.  Here's a chart showing how folks that check their units did on the question, as opposed to those that didn't:

I'm not really sure how to say it more clearly than that.

Pull-back cars redux

Here's another report from our investigation of pull-back cars:

How does the launch speed vary with ramp angle? - Cam, Mike, Toru  

The Goal:   The goal of our lab was to find the launch speed off a ramp in terms of the ramp angle. 

How'd You Do It?  We kept the distance of travel on the ramp and the distance we pulled back the car a constant. This way we could keep the function with only two variables, θ and ∆x. To get the maximum results we made the distance of travel where the car reaches near maximum speed while the car is still accelerating. This distance was found using Logger Pro. In order to give a bigger range of ∆x's, we put the ramp up on a higher location. The bigger range reduced the possible errors that could affect the calculations for the launch speed. 

What Happened?  We concluded through our experiment that in actuality any inclined angle in which the toy car has to exert a force up the slope, has a negative effect on the car's total distance traveled due to a decrease in velocity when leaving the ramp. So in the case of toy cars, the lower the angle, the farther the toy car will travel as long as the starting point is elevated above the measuring distance.

WCYDWT?: Constant Velocity Buggies

Honors Physics is wrapping up our work with the constant velocity particle model (CVPM), which is our description of how objects move with constant velocity, including several different kinds of descriptions of motion, and lots of tools to make predictions about these kinds of motions.  We've now worked with five different representations of CVPM motion:

• x vs t graphs
• v vs t graphs
• Verbal descriptions (I called them textual descriptions in the first class today, and got the expected chorus of giggles, so I gave up on that)
• Algebraic models (equations)
• Diagrams

We worked quite a bit today with algebraic and diagrammatic representations of motion, having used graphs a great deal for the past couple of weeks.

The best way to do it is to do it, so they jumped in and formulated their own questions about the two constant velocity buggies that I gave them; I took out one battery from the red one and replaced it with a strip of copper to make it run significantly slower.  They were the equipment; the question was "what can you do with this?"

They came up with great questions - some were classics, and some were a little more out-of-the-box.  All let them test their diagramming and algebraic problem-solving chops:

• Cars facing each other - "where/when will they collide?"

• Cars starting apart - "when/where will one car pass the other?"

• Cars starting together, facing away from each other - "when will they be 10 m apart?"

Not only did they solve this one algebraically, they took their extra time and solved the problem graphically as well!

• Cars starting together - "when will one car have gone twice as far as the other?" 

This was very interesting; after a great deal of wrestling with their algebra, the time interval and the distance always canceled, leaving:

 

This is a strange result indeed - no reference to time or distance!  The interpretation: if they really do start at the same spot, the question can only be answered if the faster car has twice the speed of the slower car.  If it does, then any time or distance works.  If not, no time or distance works!