Three Representations

Today the honors physics classes took their first crack at connecting three of the four representations of interactions: system schemas, free-body diagrams, and motion graphs (v vs. t in particular here).  Along with net force equations, these will be the basis of most of the rest of the year!

We had some great whiteboard meetings as we split into five groups to construct our representations and then made sure that all of each group's representations agreed in each situation.  This is good practice for looking at your own work - multiple representations not only give you multiple avenues to attack a problem, but also let you check yourself!

I encouraged them not to write these down on the sheets that I gave them with the setups, so that they can use them as independent practice later, checking back to the whiteboards for verification afterwards.

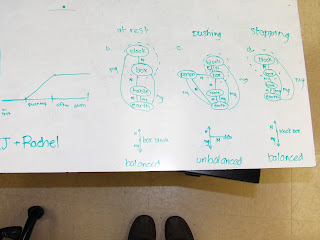
For each situation, the students evaluated each representation while the box was at rest, being pushed (and speeding up), and after it is released (after having been pushed).

The four situations were:
A rubber-bottomed cardboard box with a block inside it, on a rough floor.

A cardboard box with a block inside it, on a rough floor.

A cardboard box with a block inside it, on a smooth floor.

A cardboard box with a block inside it, on a perfectly frictionless floor.

 

 

A follow-up task for my students:

Draw v vs. t graphs for each of these four situations on the same set of axes, assuming boxes of equal weight and push forces of equal and constant size.  Here's a template, along with a color-code, ready for magic markers!

 

Along the way, we had a great discussion about what happens to our system schema if we split the box and the block inside it (leading us to our first encounter with static friction!), and about what we can't tell about the motion from free-body diagrams (like... the direction of the motion!).

Thanks to Kelly for the great springboard to this one!