AP Physics brings you some investigations of Arbor Scientific's pull-back cars! These cars are pretty neat; Arbor advertises that they provide constant acceleration that's dependent upon the distance that you pull them back.
A few general observations:
- They don't travel in super-straight lines. It can be difficult to get more than 2.5 meters or so of reliably straight travel
- The little chrome-esque accessories tend to snap off upon collisions; that is, within 10 seconds of student use
- They go a billion times (approximate measure - your mileage may vary) faster with the tops taken off, and (according to the students) also look cooler
Some insights about the cars:
Does the floor surface affect the acceleration? - Kati and Kawala
The Goal:
Our original goal was to find velocity v. time on different surfaces. Since the cars didn’t stay straight, we had to change our goal to distance v. time on different surfaces. The cars deviated too far in the end to allow the cars to go until they stopped. Our final goal was to determine the time that the car takes to travel 3m on different surfaces. We choose 3m because it was the longest part where the car stayed straight.
How'd You Do It?
We tested the car on three different surfaces: ground, table and carpet. In order to keep the car going straight, we set three meter track by using rulers as an acceptable travelling distance. The gap between the tracks was 12cm and the distance between the “pulling back” place and the start point was 36cm so that the car’s engine was well-prepared to go forward. We set up these steps as precise as we could every time we changed surfaces. We first pulled back the car to let it start on the ground and measured how long the car took to pass through the three meter track. We then did the same thing on table and carpet and recorded 8 data sets for each surface. Time was the only variable here. We figured out the relationship between the time and different surfaces from the car’s motion, and the following data and graph showed the results.
What Happened?
From our data the ground and the table’s time for the
car to go 3m is close enough for it not to be negligible. The carpet was
significantly affected the motion of the car. The data table shows the ground
was more consistent than the other materials.
How does the acceleration vary with pull-back distance? - Alex, Alex, and Brandon
The Goal:
We wanted to determine
whether two times the pull on the car will give us two times the acceleration
of the car.
How'd You Do It?
In order to figure
whether two times the pull would equal two times the acceleration, we did a
simple set-up using a motion detector at a 1 meter distance from the starting
line of the car to determine what the acceleration would be. We began with pulling the car back to a
distance of 10 cm and recording the acceleration. Next, we pulled the car back to 20 cm doubling the initial
distance, and record data from that test.
We also recorded the acceleration of the car with multiple other pull
back distances. 15cm, 30cm, 35cm,
40cm, 50cm, 60cm, 70cm, 80cm, and 100cm.
What Happened?
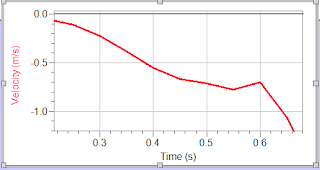
On the right is a picture of the 60 cm pullback test. Though the graph does not obviously
represent any function, we decided to approximate the slope of the line to find
the average acceleration.
Once the pull back distance
reached 70cm the car started to click.
From the data and the graph below we see that this is the maximum amount
of pullback distance and anything above has no effect.
This is the graph of the data we collected. We wanted to find a function to predict
how fast a car would accelerate for how far we pulled it back so we found this
function.
/ .275 (x) ^ .503 for
0 <
x < 70 cm
Acceleration (x drawback) =|
\ 2.15
for 70
< x
*Where x is the draw back in centimeters*
We
discovered that two times the pull back does not give two times the
acceleration. Up to 35cm pull back
twice the pull back actually gives approximately root(2) times more acceleration. We would are able to see that this is
true because of the x^.503 in our best-fit equation for the graph. We discovered another cool thing in
that once we reached 70 centimeters the car would not accelerate any faster.

No comments:
Post a Comment